Hvad bruges epicykliske gear til?

Epicykliske gearogså kendt som planetgearsystemer, anvendes i vid udstrækning i forskellige brancher på grund af deres kompakte design, høje effektivitet og alsidighed.

Disse gear bruges primært i applikationer, hvor pladsen er begrænset, men hvor højt drejningsmoment og hastighedsvariation er afgørende.

1. Biltransmissioner: Epicykliske gear er en nøglekomponent i automatgearkasser, der giver problemfri gearskift, højt drejningsmoment ved lave hastigheder og effektiv kraftoverførsel.
2. Industrimaskiner: De bruges i tunge maskiner på grund af deres evne til at håndtere høje belastninger, fordele drejningsmomentet jævnt og fungere effektivt i kompakte rum.
3. Luftfart: Disse gear spiller en afgørende rolle i flymotorer og helikopterrotorer og sikrer pålidelighed og præcis bevægelseskontrol under krævende forhold.
4. Robotik og automatisering: Inden for robotteknologi bruges epicykliske gear til at opnå præcis bevægelseskontrol, kompakt design og højt drejningsmoment i begrænsede rum.

Hvad er de fire elementer i det epicykliske gearsæt?

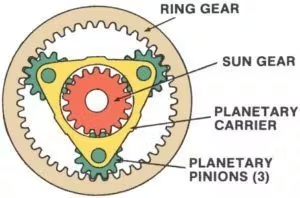
Et epicyklisk gearsæt, også kendt som etplanetgear system, er en yderst effektiv og kompakt mekanisme, der almindeligvis anvendes i biltransmissioner, robotteknologi og industrimaskiner. Dette system består af fire nøgleelementer:

1. SoludstyrSolhjulet, der er placeret i midten af ​​tandhjulssættet, er den primære driver eller modtager af bevægelse. Det er i direkte indgreb med planethjulene og fungerer ofte som systemets input eller output.

2. PlanetgearDisse er flere gear, der roterer omkring solhjulet. De er monteret på en planetgearkasse og går i indgreb med både solhjulet og ringhjulet. Planethjulene fordeler belastningen jævnt, hvilket gør systemet i stand til at håndtere et højt drejningsmoment.

3.PlanetbærerDenne komponent holder planethjulene på plads og understøtter deres rotation omkring solhjulet. Planethjulsholderen kan fungere som et input-, output- eller stationært element afhængigt af systemets konfiguration.

4.RinggearDette er et stort ydre tandhjul, der omgiver planethjulene. Ringhjulets indvendige tænder går i indgreb med planethjulene. Ligesom de andre elementer kan ringhjulet fungere som input, output eller forblive stationært.

Samspillet mellem disse fire elementer giver fleksibiliteten til at opnå forskellige hastighedsforhold og retningsændringer inden for en kompakt struktur.

Hvordan beregner man gearforholdet i et epicyklisk gearsæt?

Gearforholdet for enepicyklisk gearsæt afhænger af hvilke komponenter der er faste, input og output. Her er en trinvis vejledning til beregning af gearforholdet:

1. Forstå systemkonfigurationen:

Identificér hvilket element (solen, planetbæreren eller ringen) der er stationært.

Bestem input- og outputkomponenterne.

2. Brug den grundlæggende gearforholdsligning: Gearforholdet for et epicyklisk gearsystem kan beregnes ved hjælp af:

GR = 1 + (R / S)

Hvor:

GR = Udvekslingsforhold

R = Antal tænder på ringhjulet

S = Antal tænder på solhjulet

Denne ligning gælder, når planetbæreren er udgangen, og enten solen eller ringhjulet er stationært.

3. Juster til andre konfigurationer:

• Hvis solhjulet er stationært, påvirkes systemets udgangshastighed af forholdet mellem ringhjulet og planethjulet.
• Hvis ringhjulet er stationært, bestemmes udgangshastigheden af ​​forholdet mellem solhjulet og planetbæreren.

4. Omvendt gearforhold for output til input: Når man beregner hastighedsreduktion (input højere end output), er forholdet ligetil. For hastighedsmultiplikation (output højere end input) skal man invertere det beregnede forhold.

Eksempelberegning:

Antag at et gearsæt har:

Ringgear (R): 72 tænder

Solgear (S): 24 tænder

Hvis planetbæreren er udgangen, og solhjulet er stationært, er udvekslingsforholdet:

GR = 1 + (72 / 24) GR = 1 + 3 = 4

Det betyder, at udgangshastigheden vil være 4 gange langsommere end indgangshastigheden, hvilket giver et reduktionsforhold på 4:1.

Forståelse af disse principper gør det muligt for ingeniører at designe effektive og alsidige systemer, der er skræddersyet til specifikke applikationer.