Som transmissionsmekanisme anvendes planetgear i vid udstrækning i forskellige tekniske praksisser, såsom gearreduktioner, kraner, planetgearreduktioner osv. Planetgearreduktioner kan i mange tilfælde erstatte transmissionsmekanismen i et fastakslet tandhjulstog. Da geartransmissionen er i linjekontakt, vil langvarig indgreb forårsage gearfejl, så det er nødvendigt at simulere dets styrke. Li Hongli et al. brugte den automatiske indgrebsmetode til at indgribe planetgearet og opnåede, at drejningsmomentet og den maksimale spænding er lineære. Wang Yanjun et al. indgreb også planetgearet ved hjælp af den automatiske genereringsmetode og simulerede statik og modal simulering af planetgearet. I denne artikel bruges tetraeder- og hexaederelementer primært til at opdele indgrebet, og de endelige resultater analyseres for at se, om styrkebetingelserne er opfyldt.

1. Modeloprettelse og resultatanalyse

Tredimensionel modellering af planetgear

PlanetgearBestår hovedsageligt af ringgear, solgear og planetgear. De vigtigste parametre, der er valgt i denne artikel, er: antallet af tænder på den indre tandkrans er 66, antallet af tænder på solgearet er 36, antallet af tænder på planetgearet er 15, den ydre diameter af den indre tandkrans er 150 mm, modulet er 2 mm, trykvinklen er 20 °, tandbredden er 20 mm, addendumhøjdekoefficienten er 1, slørkoefficienten er 0,25, og der er tre planetgear.

Statisk simuleringsanalyse af planetgear

Definer materialeegenskaber: Importer det tredimensionelle planetgearsystem, der er tegnet i UG-softwaren, til ANSYS, og indstil materialeparametrene som vist i tabel 1 nedenfor:

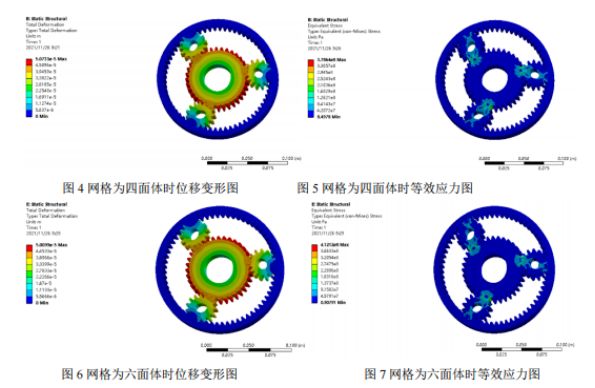
Netværk: Finite element-nettet er opdelt i tetraeder og hexaeder, og elementets grundstørrelse er 5 mm. Daplanetgear, solhjulet og den indre tandhjulsring er i kontakt og går i indgreb, nettet mellem kontakt- og nettet er fortættet, og størrelsen er 2 mm. Først anvendes tetraedriske gitre, som vist i figur 1. Der genereres i alt 105906 elementer og 177893 noder. Derefter anvendes et hexaedrisk gitter, som vist i figur 2, og der genereres i alt 26957 celler og 140560 noder.

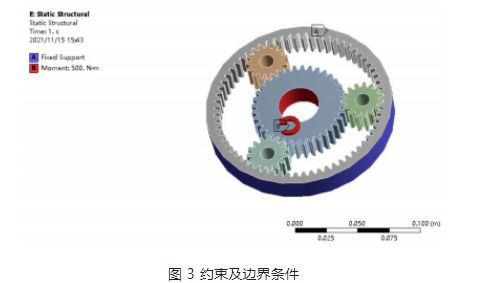
Belastningspåføring og randbetingelser: I henhold til planetgearets arbejdsegenskaber i reduktionsgearet er solgearet det drivende gear, planetgearet er det drevne gear, og den endelige udgang sker gennem planetholderen. Fastgør den indre tandkrans i ANSYS, og påfør et moment på 500 N · m på solgearet, som vist i figur 3.

Efterbehandling og resultatanalyse: Forskydningsnephogrammet og det ækvivalente spændingsnephogram fra statisk analyse opnået fra to gitterinddelinger er vist nedenfor, og der udføres en sammenlignende analyse. Ud fra forskydningsnephogrammet af de to typer gitre konstateres det, at den maksimale forskydning forekommer på det sted, hvor solhjulet ikke går i indgreb med planethjulet, og den maksimale spænding forekommer ved roden af ​​tandhjulsindgrebet. Den maksimale spænding i det tetraedriske gitter er 378 MPa, og den maksimale spænding i det hexaedriske gitter er 412 MPa. Da materialets flydegrænse er 785 MPa, og sikkerhedsfaktoren er 1,5, er den tilladte spænding 523 MPa. Den maksimale spænding for begge resultater er mindre end den tilladte spænding, og begge opfylder styrkebetingelserne.

2. Konklusion

Gennem finite element-simulering af planetgearet opnås forskydningsdeformationsnephogrammet og det ækvivalente spændingsnephogram for gearsystemet, hvorfra de maksimale og minimale data og deres fordeling iplanetgearmodellen kan findes. Placeringen af ​​den maksimale ækvivalente spænding er også det sted, hvor tandhjulets tænder har størst sandsynlighed for at svigte, så der bør lægges særlig vægt på det under design eller fremstilling. Gennem analyse af hele planetgearsystemet overvindes den fejl, der forårsages af analysen af ​​kun én tandhjulstand.